The Newsvendor Model and Apparel

The newsvendor model provides inventory planners with a framework for setting optimal order quantities when demand is uncertain and there is a limited selling window – as in seasonal apparel. Buy too little and you run the risk of early stockout and missed sales, too much and you risk write-offs and markdowns. Here, we cover:

• The classical formula for profit-maximizing order size, and also
• A numerical example for apparel. Here, the model indicates that one should typically aim to stock out by season's end about $1/3$ of the time. However, this target can increase sharply as costs rise – as they have recently with inflation and tariffs.

In practice, the optimal order quantity results we cover here may often serve as upper bounds. In apparel, for example, substitutable products can often soften the cost of stocking out on any single item. We’ll explore that dynamic in a future post.

Need help applying these formulas? VarietyIQ's demand forecasting algorithms provide all the inputs needed for ready order optimization.

Review of the basic equations

We want to decide how many units $Q$ to purchase of a product with a limited selling window – e.g., a fall sweater or other seasonal apparel item. Demand is uncertain but follows a known distribution. For simplicity, we'll assume it's normally distributed in our examples:

$$\begin{array}{c}d\sim N(\mu ,{\sigma }^2)\end{array}$$

Here, $\mu$ is the expected demand and ${\sigma }^2$ is the variance – both are values that can be estimated from past sales data. Because demand is uncertain, we always run the risk of ordering too much or too little. The optimal order quantity balances these two risks.

The newsvendor model gives the profit-maximizing order quantity. It says we should purchase up to the point $Q$ where:

$$\begin{array}{c}P(d\le Q)=\frac{c_g}{c_g+c_l}\end{array}$$

On the left is the probability that demand $d$ comes in less than or equal to $Q$. On the right:

• $c_g$ is the gain from selling one more unit (retail price minus unit cost), and
• $c_l$ is the loss from over-ordering by one unit (unit cost minus salvage value)

These are values you can look up for your business and plug in to get the optimal order quantity. E.g., if the right side of (2) exactly equals 0.5, this says we should order the median demand – equal to the expected demand in a normal distribution. If the right side is greater than 0.5, the margin is high and it pays to order more than expected demand to avoid missing out on potential sales. Finally, if it's less than 0.5, loss aversion matters more, so we should order less than the expected demand. The figure below and its caption illustrate this.

In the next section, we’ll walk through a detailed numerical example for apparel.

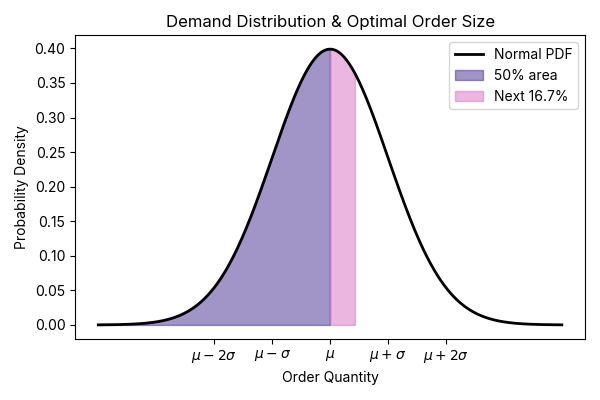
Figure: Demand distribution for a given product. The expected demand is $\mu$ units, but there is also some uncertainty set by the standard deviation $\sigma$. If the margin and salvage values lead to a critical ratio of 0.5 – as in (2) – the optimal order quantity equals the expected demand (we purchase over the dark purple area, up to $\mu$). If the ratio is 0.66 — our estimate below for the apparel industry average — the goal is to stock out only about one-third of the time. This corresponds to ordering approximately $0.4\sigma$ above the mean, covering the combined dark purple and pink shaded areas.

Typical conditions for apparel

The average gross margin for apparel is about [ref]

$$\begin{array}{c}\frac{c_g}{c_g+c_u}\approx 0.5\end{array}$$

Here, we’ve introduced $c_u$, the unit cost. This ratio (3) implies that $c_g\approx c_u$. If half the unit cost can be recovered through salvage, we then have

$$\begin{array}{c}\frac{c_g}{c_l}\approx 2\end{array}$$

Plugging this result into (2) then says that we should order up to the point $Q$ which satisfies

$$\begin{array}{c}P(d\le Q)\approx \frac{2}{3}\end{array}$$

That is, we should aim to stock out about $1/3$ of the time. Running with our normal statistics assumption, a quick numerical calculation shows that this requires ordering a quantity equal to

$$\begin{array}{c}Q\approx \mu +0.43\sigma \end{array}$$

We see then that within apparel margins are typically sufficiently high that – at least for independent products – it pays to order a little more than the expected demand, so as to avoid missing out on some potential sales if demand comes in hot.

To give a specific example to illustrate application of (6), consider a product with expected demand $\mu =500$ and uncertainty $\sigma =200$. In this case, the optimal order volume is $Q=500+0.43\times 200=590$. It’s counterintuitive (for me at least) that as uncertainty goes up, profit maximization requires ordering more here rather than less – but when the tradeoff between $c_g$ and $c_l$ favors not missing out on potential upside under hot demand – it really does [1].

Apparel under decreasing margin

How do the results above change if margins decrease?

• When retail and salvage prices increase proportionally to the average unit costs, nothing changes, as the ratio $c_g/c_l$ will remain fixed.
• However, in the opposite limit where retail and salvage prices remain fixed but average unit cost goes up, we’ll need to order less. The table below gives a summary of this scenario, showing that there is a strong sensitivity to unit costs.

We note that recent tariff and inflation costs have actually contributed to increases at the scales considered in the table below – i.e., at scales requiring quite large changes to operations! In general, retailers will respond to shocks like these by both lifting prices to some degree and also ordering somewhat more conservatively, striking a balance between the two limits above. The optimal balance will depend on each business’s unique demand elasticity.

Unit cost lift factor	$P(d\le Q)$	Optimal order size for normal stats, $Q$
$10\%$	$0.6$	$\mu +0.25\sigma$
$25\%$	$0.5$	$\mu$
$50\%$	$0.33$	$\mu -0.43\sigma$

Table: How optimal order quantity changes in apparel when unit costs rise, but retail and salvage values are held constant. For example, the middle row shows that a $25\%$ increase in unit cost lowers the optimal order to the expected demand — implying it’s optimal to shoot for a 50% stockout rate by season’s end, vs the initial $33\%$ intended stockout rate. This is based on (2), with $\frac{2-1.25}{1.25-0.5}=0.5$.

Discussion

Here, we have reviewed the newsvendor model, a practical framework for determining optimal order quantities under uncertain demand and limited selling windows – conditions that apply to seasonal apparel. Our analysis suggested that with typical apparel gross margins (~50%), businesses should plan to stock out roughly one-third of the time. However, we also covered how these baselines might shift sharply with decreases to margin.

While the newsvendor model provides useful intuition, it doesn’t include all concerns affecting a real business. First, it treats each product in isolation, ignoring substitutability between similar items – this dynamic is near to our hearts, and we plan to address this in a future post. Second, many retailers have the ability to chase in-season, placing follow-up orders based on early performance. Both of these effects favor decreasing initial order sizes.

The newsvendor model attempts to balance the costs that result from uncertainty in demand. A complementary approach one can take to alleviate these costs is to work towards reducing this uncertainty in the first place. VarietyIQ’s inventory curation algorithm can help to achieve that goal by balancing inventory across demand segments – stabilizing demand for individual products via the reduction of internal competition.

This concludes our series reviewing classical ordering theory!

Appendix: Derivation of (2)

If we buy into the $Q+1$’st item, the expected gain of that unit purchase is

$$\begin{array}{c}{c}_g\times [1-P(d\le Q)]\end{array}$$

This is the gain of a sale times the chance demand will be at least $Q+1$, so that the new unit will sell. Similarly, the expected loss on this item is

$$\begin{array}{c}{c}_l\times P(d\le Q)\end{array}$$

To maximize total expected value, we want to buy up to the point where the expected gain of adding a new unit is first no larger than the expected loss of adding that unit. At that point, (1) and (2) are equal, so

$$\begin{array}{c}{c}_g\times [1-P(d\le Q)]=c_l\times P(d\le Q)\end{array}$$

Rearrangement gives (2), the result we quoted above.

---

Thanks to Jaireh Tecarro for once again creating the banner image for our post.

[1] We see that when margin is high, profit is maximized by ordering more than expected demand. Summing over all products, this effect can lead to meaningful levels of physical waste. One way to reduce waste then is to work towards reducing demand uncertainty. As we highlight in the discussion section, one option we support at VarietyIQ is improved curation, which can help to reduce internal competition between products, stablizing demand.